Deploying ModernBERT on Apple Neural Engine

How to make it both fast and accurate • January 14, 2025

The recently released ModernBERT model is exciting. It takes several advances from recent decoder-only LLMs (think Llama, ChatGPT) and applies them to the encoder-only model that started it all: BERT.

BERT-style models don't generate text but they are adept at understanding it. You can adapt (finetune) them for your custom problems, and they are small which makes them easy to deploy.

They are small enough in fact that you can even embed them in an app and have them run on your phone.

Apple devices all come with a special chip, the Apple Neural Engine (ANE), that is ideal for this type of model. Let's see what it takes to get it running!

(Spoiler: if you've done this before, it's trickier than you might expect.)

Baseline

Let's do the bare minimum as a starting point. We can take the official model from HuggingFace and use Apple's coremltools to convert it to CoreML format. This format is required to utilize the ANE hardware.

Conversion is straightforward:


from transformers import AutoModelForMaskedLM
import torch
import coremltools as ct
import numpy as np

class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.model = AutoModelForMaskedLM.from_pretrained(
            "answerdotai/ModernBERT-base"
        )
    def forward(self, input_ids, attention_mask):
        return self.model(
            input_ids=input_ids,
            attention_mask=attention_mask).logits

model = Model().eval()
input_ids = torch.zeros((1, 1024), dtype=torch.int32)
mask = torch.ones_like(input_ids)
ct.convert(
    torch.jit.trace(model, (input_ids, mask)),
    inputs=[
        ct.TensorType(name="input_ids",
                      shape=input_ids.shape,
                      dtype=np.int32),
        ct.TensorType(name="attention_mask",
                      shape=mask.shape,
                      dtype=np.int32,
                      default_value=mask.numpy()),
    ],
    outputs=[ct.TensorType(name="logits")],
    minimum_deployment_target=ct.target.macOS14,
).save(f"ModernBERT-base-hf.mlpackage")

We can open the resulting model in Xcode and run a benchmark to see how fast it is.

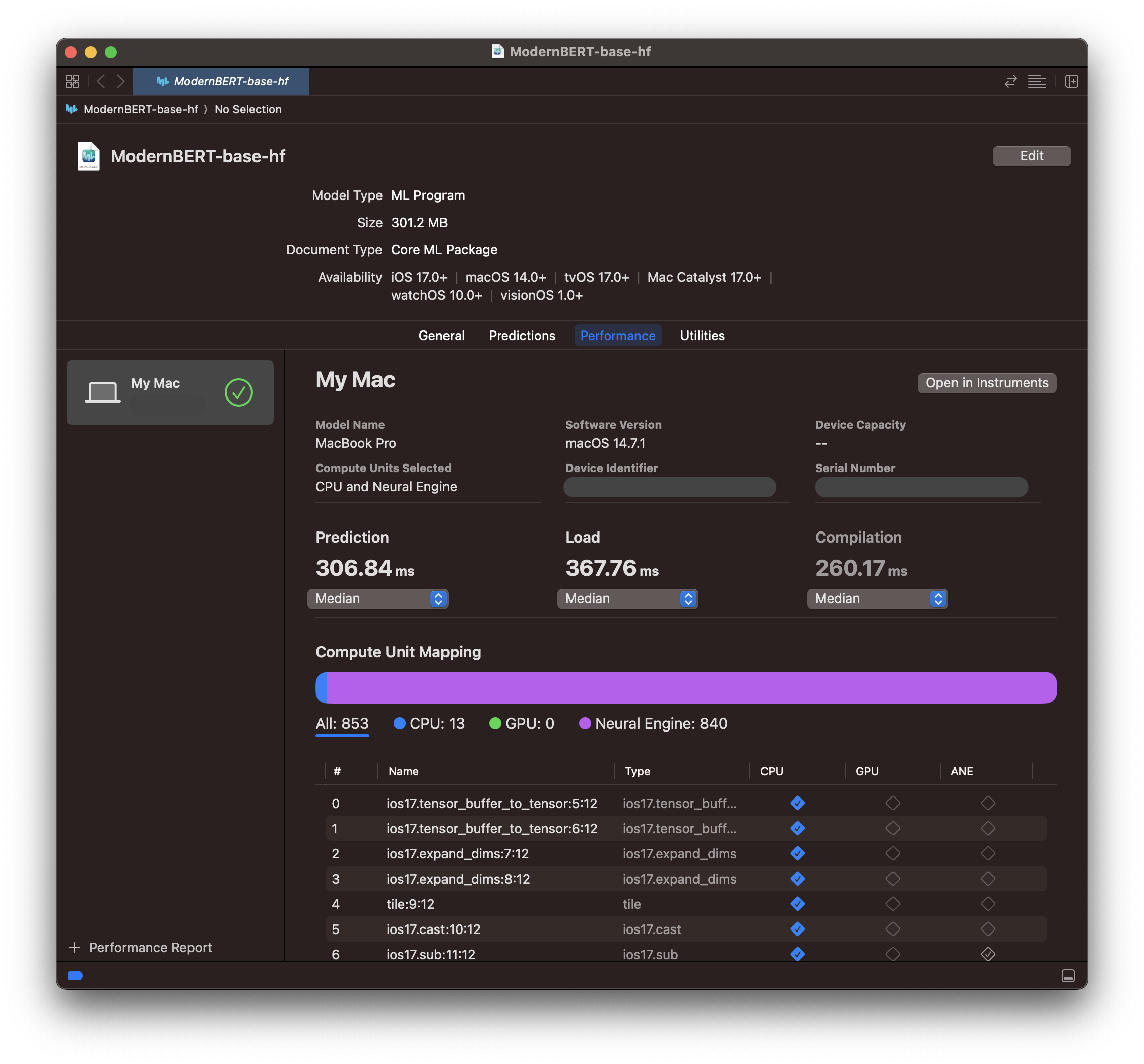Xcode benchmark results for baseline huggingface ModernBERT CoreML model

_{Focus on: Median prediction time (small=good). Compute unit mapping (purple=good).}

These are solid results considering we've barely done anything so far. Almost the entire model runs on ANE and it's reasonably fast. Surprisingly, if we open the performance report in Instruments, we can see that >40% of the model's latency comes from the few operations that don't execute on ANE. So the ANE portion is much faster than it initially seemed!

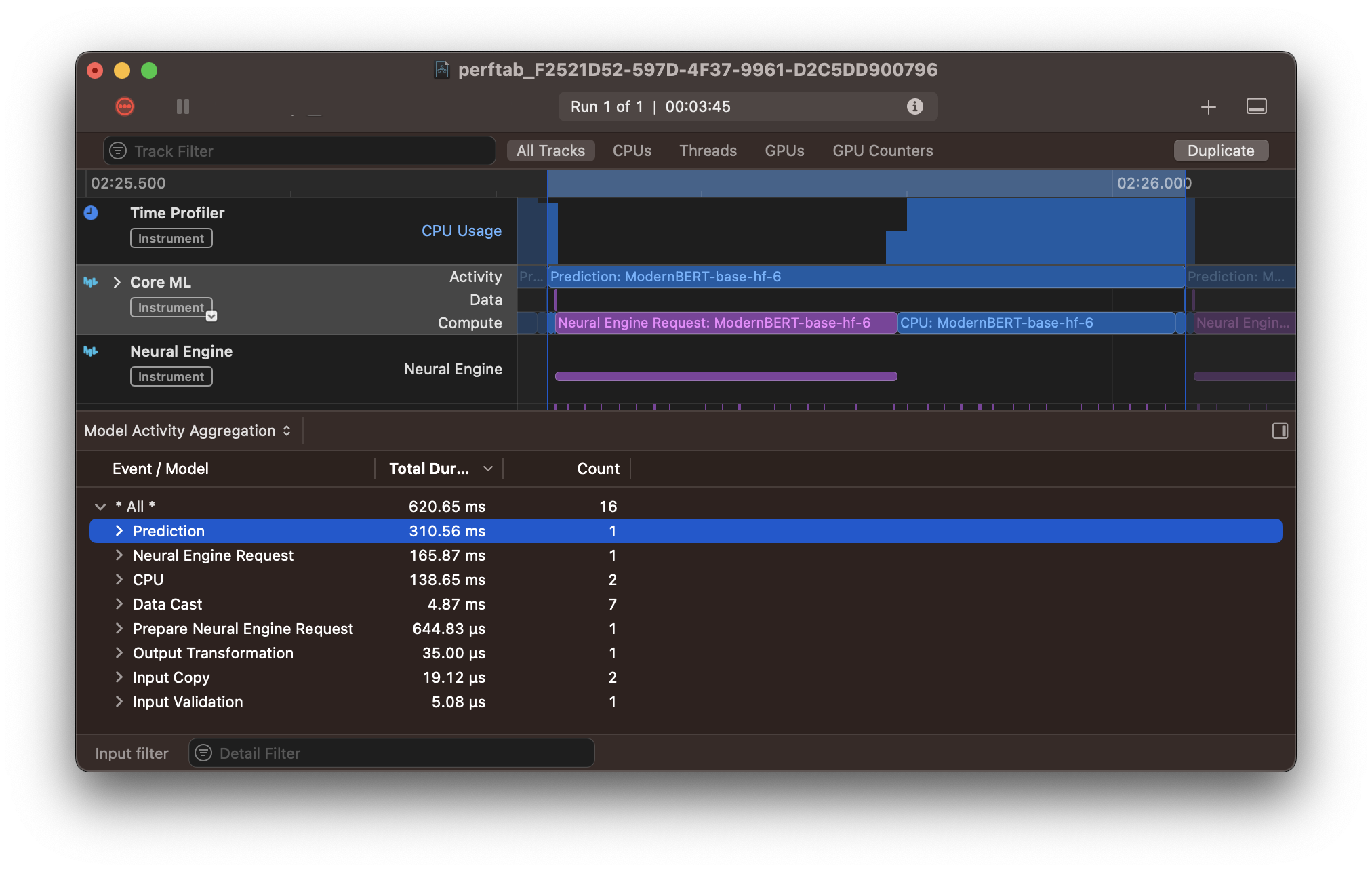Xcode benchmark Instruments trace for baseline huggingface ModernBERT CoreML model

_{Representative prediction of the HF model. Notice: the CPU compute (large blue block) takes 138 of the 310ms! Most of the actual computation happens in 165ms on the Neural Engine.}

Let's improve on this.

Hardware Optimizations

CoreML automatically optimizes models for efficient performance. Since we want to specifically target the ANE hardware, we will make modifications to further improve performance there.

The baseline HuggingFace implementation offers niceties like customizability and GPU optimizations. These aren't important for ANE so to make things easier we will re-implement the model in a single file a la nanoGPT.

The standard reference for this is Apple's 2022 post "Deploying Transformers on the Apple Neural Engine" which we will follow closely.

The main change is replacing all linear layers with 2D convolutions. Both can perform the matrix multiplications we need, but the ANE is better at convolutions.

Hand-in-hand with this, we will update all our inputs to be 4D tensors (think 4D matrix).

The HF model uses a linear layer to transform a 3D input tensor with shape (Batch, Sequence, Channel Input) to (B,S,Channel Output) using a learned weight matrix (Cout,Cin). Our equivalent convolution will transform a 4D tensor (B, Cin, 1, S) to (B,Cout,1,S) using a weight (Cout,Cin,1,1).

As you can see the resulting tensor shapes are the same, only in a different order.

These changes alone speed up the model, but we will also adopt the custom attention implementation detailed in the post for an additional speedboost.

We can confirm our re-implemented model is correct by comparing the output of our model to the HF model using a metric called KL Divergence. This measures the similarity of two distributions and a very small number is good.


❯ python diff_torch.py
comparing answerdotai/ModernBERT-base to 🤗
# …
kl div: ± 9.7043e-08
_{9.7e-08 is 0.000000097043}

For a more subjective comparison, we can look at the model's top predictions for the sentence "The ocean is full of [MASK].":

Probability	[MASK] Replacement
0.1060	life
0.0593	sharks
0.0507	people
0.0406	fish

These are all reasonable completions, and their probabilities match the HF model exactly. Our new PyTorch model is looking good.

Speed and Accuracy

We can convert our new optimized PyTorch model to CoreML just like before. As expected, it is faster: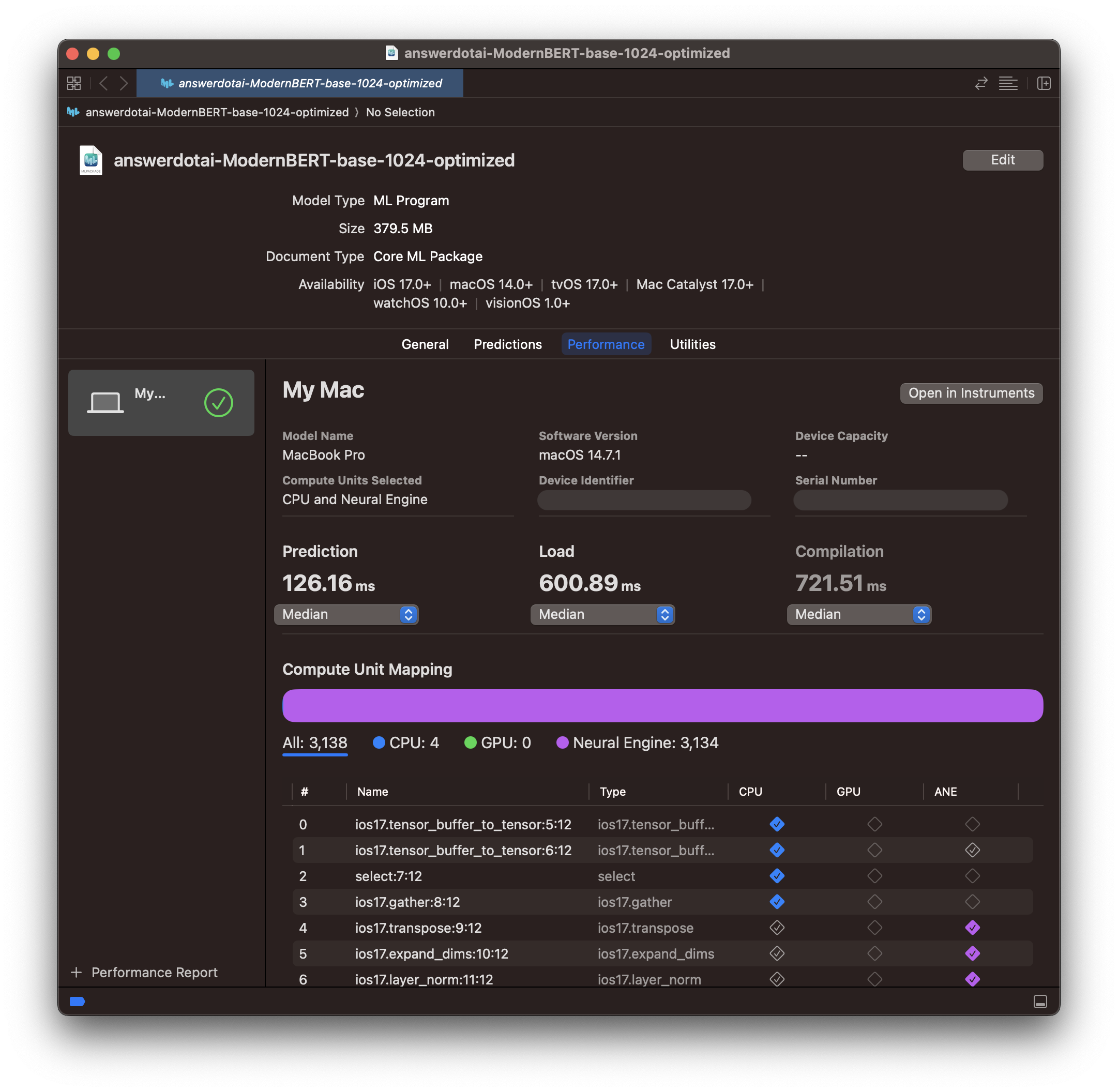 Xcode benchmark results for ANE-optimized ModernBERT CoreML model

Xcode benchmark results for ANE-optimized ModernBERT CoreML model

_{Faster and more purple.}

Looking at the performance report explains why. The large chunk of CPU computation we were doing at the end of the model has moved from CPU to ANE (the final blue CPU block is absent from the report). Despite this extra computation, the ANE section is also ~20% faster (165ms → 123ms).

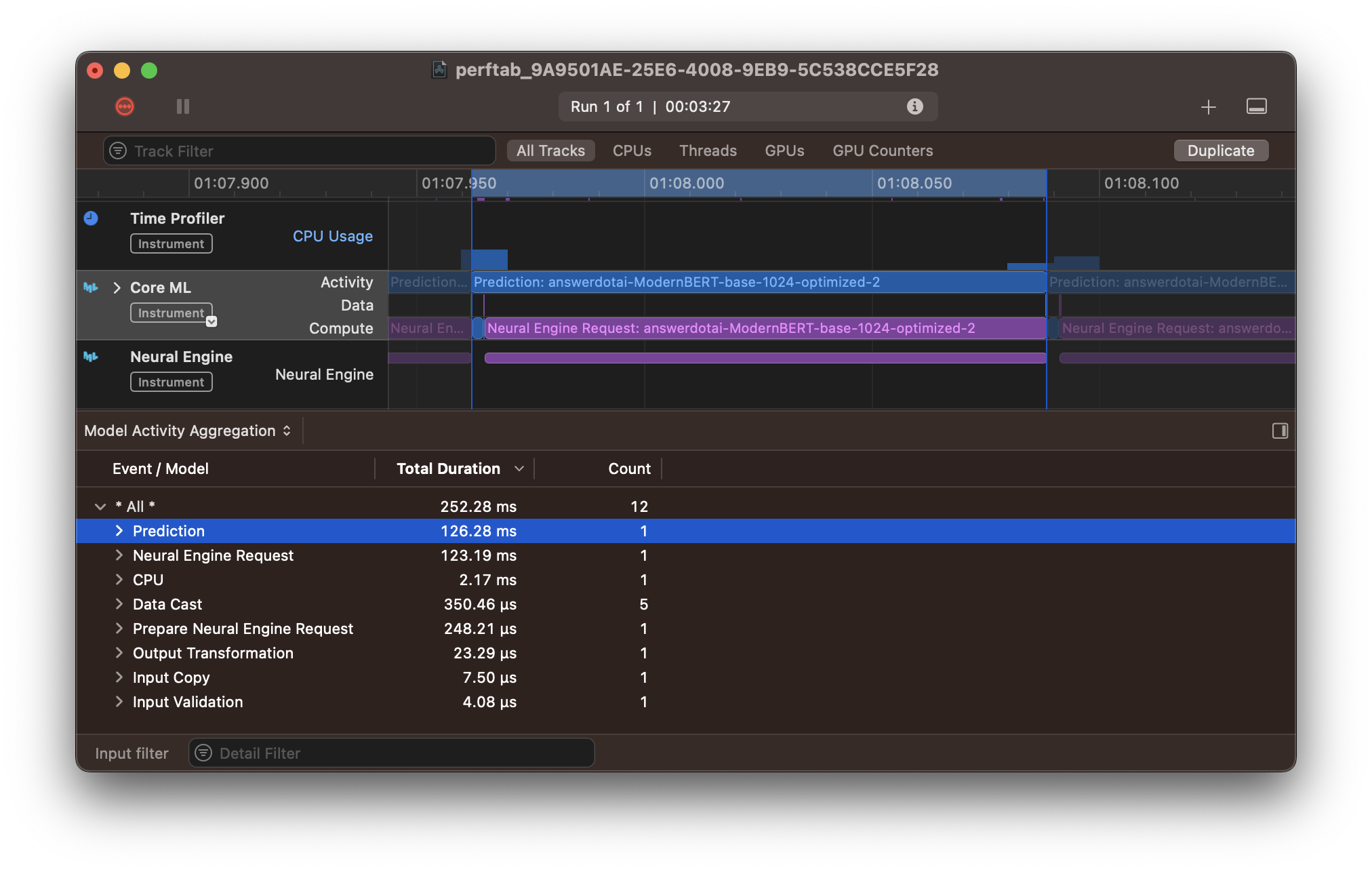Xcode benchmark Instruments trace for ANE-optimized ModernBERT CoreML model

_{Instruments trace of a representative prediction with the optimized model.}

So speed is good, what about accuracy? Let's check the KL divergence of our CoreML model and HuggingFace.


❯ python diff_coreml.py answerdotai-ModernBERT-base-1024-optimized.mlpackage "The ocean is full of [MASK]."
KL Divergence
Sequence only (excl. padding): 4.35444974899292
_{or 4.35e0}

Oh no! This is many orders of magnitude larger. Our model is fast but it has lost some accuracy.

We can check this subjectively by looking at the same sentence from before "The ocean is full of [MASK].":

Probability	[MASK] Replacement	Δ (%) to HF Probability
0.0644	people	+0.0137 (+27%)
0.0596	life	-0.0464 (-43%)
0.0394	sharks	-0.0199 (-33%)
0.0373	fish	-0.0033 (-8%)

"life" is no longer the top prediction and the probabilities have shifted noticeably.

Outliers

One feature of the ANE is that it uses float16 for computation.

float16 can only express numbers between -65k and +65k and the closer you get to those large values, the less accurate. (Floating point numbers work by only representing a finite subset of all possible numbers and that subset gets more spread out as values approach the extremes.)

These types of errors tend to compound in ML models, so they are a prime suspect for what we're seeing.

Fortunately they also tend to show up in predictable places for modern LLMs. We can simply print the maximum values for an example sentence to see what they look like.


class Block(nn.Module):
    # …
    def forward(self, x, position_ids, attention_mask, sliding_window_mask=None):
        print(f"layer {self.layer_index} max: {x.abs().max().item()}")
        # …
        _{This is one of the places that large values can appear.}

For "The capital of France is [MASK]." we get:


layer 0 max: 8.465672492980957
layer 1 max: 21.899389266967773
# …
layer 11 max: 423.6680908203125
layer 12 max: 9862.669921875
# …
layer 20 max: 19701.166015625
layer 21 max: 19706.68359375

Just as expected, about halfway through the model we start to see large values that grow up to 20-30k, depending on the input text.

Let's compare this with the original BERT.


layer 0 max: 11.113615989685059
layer 1 max: 10.009736061096191
layer 2 max: 11.489322662353516
layer 3 max: 14.738886833190918
layer 4 max: 13.510597229003906
layer 5 max: 13.328920364379883
layer 6 max: 14.002219200134277
layer 7 max: 13.596477508544922
layer 8 max: 14.410932540893555
layer 9 max: 14.204751014709473
layer 10 max: 14.246857643127441
layer 11 max: 15.104483604431152

These are much lower. This is very likely our problem.

Reducing Outliers with Rotations

Similar to how ModernBERT was trained using recent advances in decoder-only LLMs, we can borrow a technique used to quantize (compress) LLMs that should help with our outliers.

Outliers makes quantization tricky, so there are many different papers and approaches. One is particularly appealing.

Outliers show up due to the values in the learned weight matrices. For "reasons" models tend to settle on weight matrices that promote outliers in a few parts of the tensors the model is processing.

If our linear layer (or, equivalently, convolution) has a weight matrix W, and our input is a tensor X, then we can write the operation to compute the output Y as:


Y = X @ W
_{@ is the PyTorch symbol for matrix multiplication}

The trick we will use to reduce outliers comes from two papers written at the same time: QuaRot and SpinQuant.

Both use a special kind of matrix, an orthogonal rotation matrix, that has a property such that: Q @ Q.T = I. This means that multiplying the rotation matrix Q by its transpose (flipped across the diagonal) gives us the identity matrix I.

Since any matrix times I is itself, this allows us to rewrite our linear layer as:


Y = X @ I @ W
  = X @ Q @ Q.T @ W
  = (X @ Q) @ (Q.T @ W)
  = X' @ W'

As long as we make sure that our new input to the linear layer is X' (original X times Q), we can replace the original weight with W' (Q.T times original W).

Another fun property of Q is that when we multiply other matrices by it, it reduces the outliers by "smearing" them across nearby non-outlier values.

So if we multiply all the weight matrices in our model by Q or Q.T in such a way that the Qs always cancel out, we should see lower outliers but still have a mathematically equivalent model. Pretty cool.

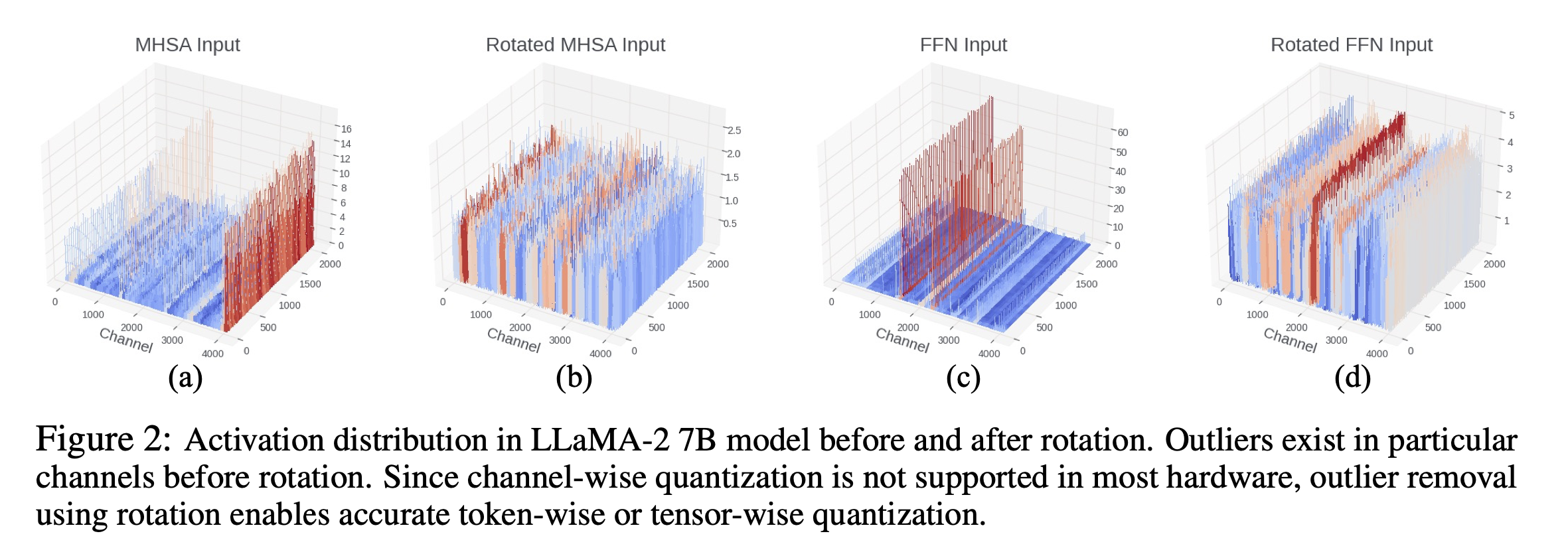3D plot of activation magnitudes before and after rotation from the SpinQuant paper

_{From the SpinQuant paper. Notice the vertical axes go from 16 → 2.5 and 60 → 5 respectively.}

A LayerNorm-Shaped Wrinkle

Unfortunately ModernBERT made two slightly contrarian choices that will make our lives a little tricky.

Most modern LLMs use a normalization function called RMSNorm. ModernBERT uses a different one, LayerNorm. QuaRot and SpinQuant only work for RMSNorm models.

The good news is that they provide a method to convert LayerNorm models into mathematically equivalent RMSNorm models.

The bad news is that this method won't work out of the box for us because of where ModernBERT puts its first LayerNorm.

Most models perform the first norm immediately before the first attention computation:


x = x + attention(layer_norm(x))

But ModernBERT does it slightly earlier:


x = layer_norm(x)
x = x + attention(x)

If you are visually inclined, the difference is easy to spot when you look at the model graph for ModernBERT and compare it to a model that follows the more common practice:

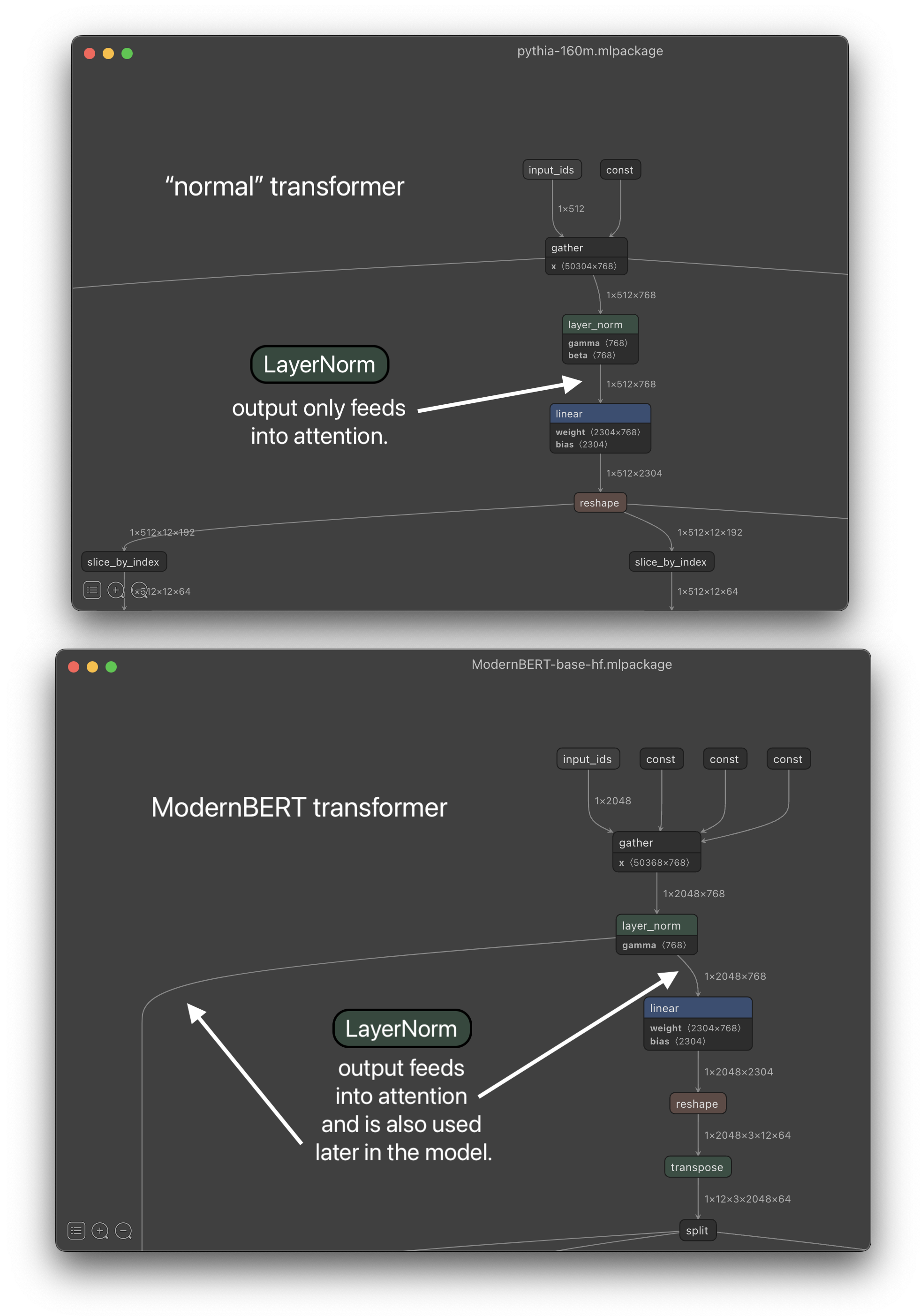netron graph of layernorm in normal transformer and modernbert

_{QuaRot+SpinQuant only describe how to handle the "normal" transformer case.}

Naively wedging this LayerNorm into the same conversion method as the others destroys the model's mathematical equivalence and its outputs. If we work the math out by hand (which I will spare you) we can actually find a way to make it work by inserting a single extra matrix multiplication in the form of a convolution:


x = rms_norm(x)
residual_x = x @ R
x = residual_x + attention(x)

The R matrix performs the operations that we would lose otherwise when replacing the LayerNorm with RMSNorm. An extra convolution would be nice to avoid, but its cost is relatively small compared to the rest of the model (only 0.19% of the model parameters).

Most importantly it allows us to apply the Q matrix to reduce our outliers.

Rotated CoreML Model

Now we can take our original model, replace all LayerNorms with RMSNorm, insert our single extra convolution, and then replace all convolution weights with versions that are multiplied by the rotation matrix Q.

We can see it closely matches the HF model:


❯ python diff_torch.py
comparing answerdotai/ModernBERT-base to 🤗
# …
kl div: ± 1.0101e-07

Even though the rotated model is mathematically equivalent, we don't expect a perfect match in practice due to floating point errors. This lines up with the KL divergence we see.

When we convert it to CoreML as before, we can see that our CoreML-to-HF KL divergence is much improved:


❯ python diff_coreml.py answerdotai-ModernBERT-base-1024.mlpackage "The ocean is full of [MASK]."
KL Divergence
Sequence only (excl. padding): 0.00017806502000894397
_{this is 1.78e-4}

And for our test sentence "The ocean is full of [MASK].", the order now matches HF and the probabilities are much closer:

Probability	[MASK] Replacement	Δ (%) to HF Probability
0.1058	life	-0.0002 (-0.1%)
0.0617	sharks	+0.0024 (+4%)
0.0496	people	-0.0011 (-2%)
0.0408	fish	+0.0002 (+0.4%)

Excellent! Examining the outliers again, we can also see that they are greatly reduced (though still larger than BERT):


layer 0 max: 3.542017936706543
layer 1 max: 4.122846603393555
# …
layer 11 max: 66.40872955322266
layer 12 max: 769.3683471679688
# …
layer 20 max: 1025.390869140625
layer 21 max: 1023.6306762695312

The Xcode benchmark results are also still just as fast. It seems the extra convolution has negligible cost.

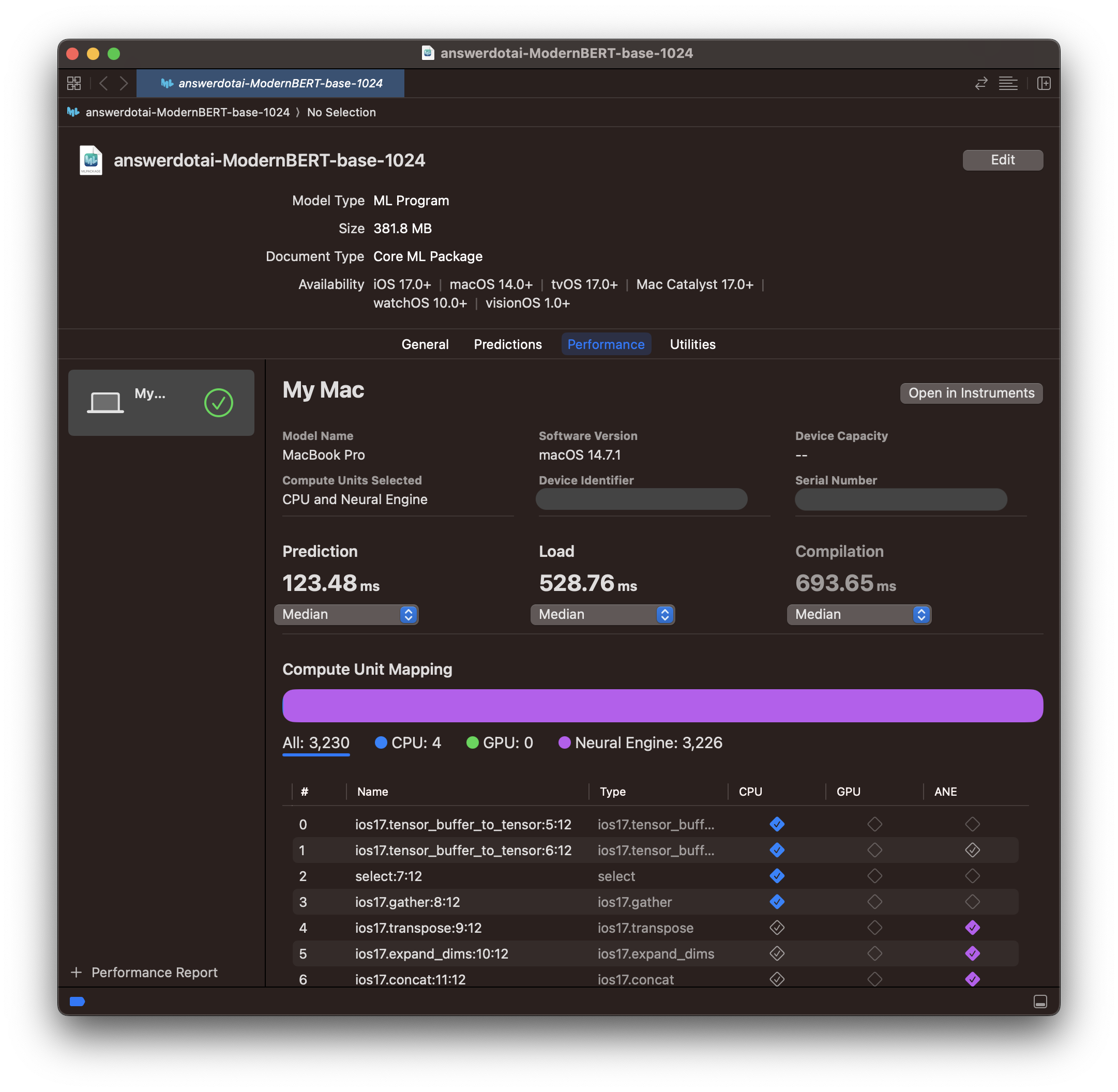Xcode benchmark results for ANE-optimized ModernBERT CoreML model with rotations

_{Same speed, same purple.}

Now we have a model that is both fast and accurate!

What's Now/What's Next

This is a solid starting point for ModernBERT on Apple Neural Engine.

The code to convert and use your own CoreML models is available on GitHub. Part of the motivation for re-implementing it in the nanoGPT-style was to make it easily hackable. The README has ideas for several areas that could be explored or improved.

The most exciting one to me is adding support for different model heads. These are what allows BERT-style models to adapt to different tasks and makes them actually useful.

Feel free to reach out to me on twitter or GitHub if this is interesting to you!